CONS-TD
The project aims to develop some contributions to the theory of delayed differential equations (DDE) and switched systems by developing, mainly, necessary and sufficient conditions for stability of equilibrium points and reducing the conservativeness of sufficient conditions given by the use of multiple Lyapunov-Krasovskii functionals.
Technical details
UEFISCDI Program: National Research-Development and Innovation Plan 2015 – 2020 (PNCDI III)
Program 1: Development of the national research-development system
Subprogram 1.1: Human Resources
Project Code: PN-III-P1-1.1-PD-2021-0610
Acronym: CONS-TD
Adjacent, the purpose of the project is to elaborate mathematical models for linear and nonlinear systems specific to the aerospace field, namely modeling an airplane wing to ensure flight stability in the presence of command line time-delays and switches between different command laws. Therefore, a secondary goal, but as important as the main goal, is to obtain classical control laws (LQG), as well as from the new generation of artificial intelligence (fuzzy logic and neural networks), in the perspective of counteracting the effects induced by time-delays. The delay, on state or on control (actuator), can lead to instability or poor performance of the control law. However, with a proper choice, the time-delay can be turned into a benefit by playing an important role in attenuating the vibrations of aeroelastic structures like wing with aileron.
Results – Phase I
Phase 1 „Preliminary studies on the stability conditions for linear and nonlinear systems of differential equations with delay and switching and ways to reduce the conservatism of these conditions” includes the following activities: Act 1.1 – State-of-the-art regarding the stability conditions of systems of differential equations with delay and switching; Act 1.2 – Evaluation of the degree of conservatism.
A first representative model considered is that of a linear system with delay, with disturbance
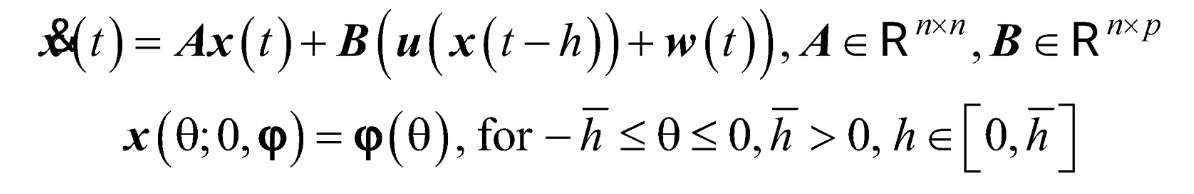
A second model is of a perturbed linear system with delay in control and controllable time-dependent switching (both models can describe the chain of command of the flight of the aircraft)
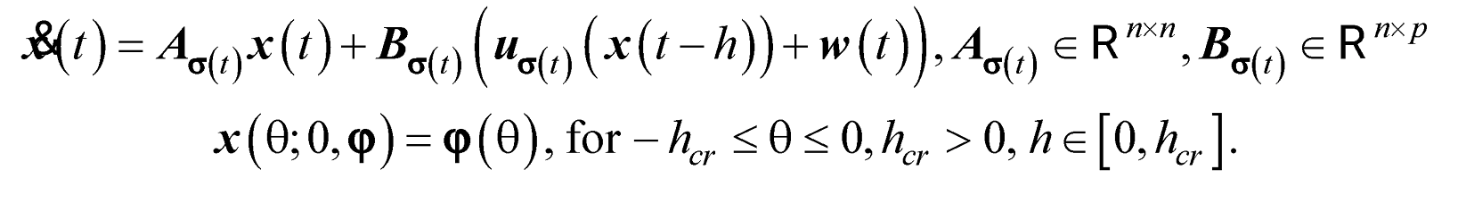
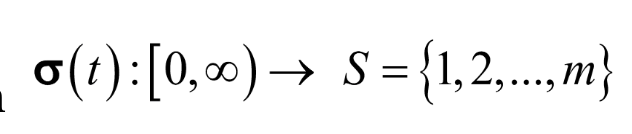
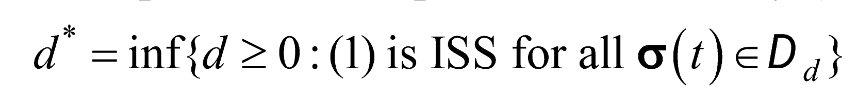
The Lyapunov Krasovskii functional (LKF) is the mathematical tool frequently used in the study of stability. During Phase I, a stability theorem (ISS) was obtained for system (1) and an ISS stability theorem taken from the literature was analyzed. The demonstration mechanism is laborious and leads to more or less conservative stability conditions. A first conclusion is that on this LKF path it is unlikely, if not impossible, to obtain non-conservative stability conditions. A suggestion of the difficulty can be seen from the fact that the problem can be put in the form of a multi-objective optimization problem with constraints: minimize
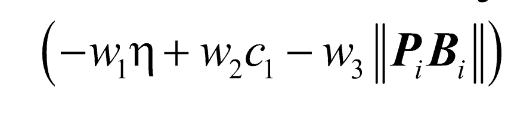
subject to:
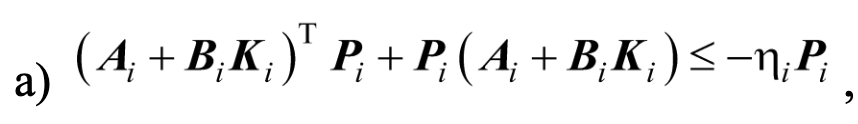
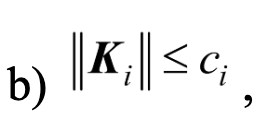
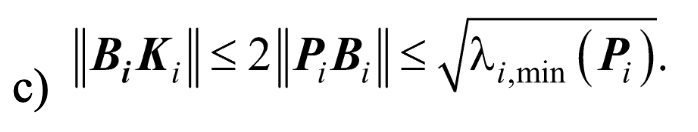
A second conclusion is that of a paradigm shift: a method to develop the suggestions coming from some works such as [G. Chesi, P. Colaneri, J. C. Geromel, R. Middleton and R. Shorten, “A Nonconservative LMI Condition for Stability of Switched Systems with Guaranteed Dwell Time]. The method uses homogeneous polynomial Liapunov functions, an idea originating in Hilbert’s famous Problem No. 17. A second way to be developed starts from the convexification of some conditions (W. Xiang et al., Nonconservative lifted convex conditions for stability of discrete-time switched systems under minimum dwell-time constraint, IEEE Transactions on Automatic Control, Volume: 64, Issue: 8, August 2019).
Results dissemination
1. Critical case of stability for a nonlinear switched system of delay differential equations with applications to a hydraulic servomechanism – D. Enciu, A. Halanay, I. Ursu, 11th International Conference on Pure and Applied Mathematics (ICPAM 2022), 12-22 July 2022, Bratislava, Slovakia
Abstract
In this paper the complex problem of nonlinear dynamical system with simultaneously critical case for stability, time-delay on state, and an autonomous uncontrolled state dependent switching rule is addressed. A general theorem ensuring simple stability for this type of system is given. This leads to the application of a Malkin-type mathematical apparatus, combined with the use of multiple complete Lyapunov-Krasovskii functionals. Since the characteristic equation of the linear approximation has a null eigenvalue, following some transformations of variables, the initial system consisting of five nonlinear differential equations is decomposed in the canonical form of Malkin approach which consists of a fourth order system and a first order system that contains only nonlinear terms. The equilibrium stability condition of the nonlinear system returns to the fulfillment of the asymptotic stability condition of the linearized equations and the Lyapunov conditions.The mathematical model is applied to the analysis and synthesis of electrohydraulic servomechanism. This real world object is vital for flight safety being an essential equipment in aircraft flight controls. Thus, some thresholds of admissible delay for ensuring the stability of the servomechanism are determined.
2. New strategy for the safety and comfort of the passengers and aircraft crew during atmospheric turbulence – D. Enciu, I. Ursu, G. Tecuceanu, 7th European Conference on Structural Control (EACS 2022), 10-13 July 2022, Warsaw, Poland
Abstract
An airplane trip can be psychological terrifying for any traveler. If, during the flight, the airplane meets a turbulent air front, then the scenario is perfect for a Hollywood movie, and the panic among passengers increases proportionally with the severity of the turbulence. In this paper, a new approach of the turbulence mitigation methodology is proposed based on a solid background using an active control vibration. The experimental model is represented by a realistic, elastic airplane wing model controlled by an electric linear servoactuator. The mathematical model is completed by numerical simulations and experiments in the subsonic wind tunnel upgraded with a turbulence generator. The qualification of an emergent technology of this type will have double impact: for the passengers – safety and mental comfort increasing given by the significant reduction of the dynamic effects produced by the turbulent field; for the airplane – weight optimization based on the loads control generated by the atmospheric turbulence.
3. A critical case for stability in a model of an electrohydraulic servomechanism – D. Enciu, A. Halanay, I. Ursu, 29th Conference on Applied and Industrial Mathematics (CAIM 2022), 25-29 August 2022, Chisinau, Republica Moldova
Abstract
In this paper, the conditions required for the stability of a nonlinear system with time-delay and switching are studied. The starting point of the theory is based on a real-world mathematical model of an electrohydraulic servomechanism located in ailerons flight controls of the Romanian IAR 99 Hawk jet training airplane. For this model, a general theorem on the equilibrium stability in a critical case for a switched nonlinear system of delay differential equations is stated. The framework uses multiple complete Lyapunov-Krasovskii functionals. The characteristic equation has one zero root which claims the use of a special approach given by a Lyapunov-Malkin theorem. Therefore, some transformations are made to write the linearized system in a canonical form where the stability Lyapunov theorem of the linear approximation can be applied. The study of the stability of equilibria relies on two conditions: a Lyapunov condition and an asymptotic stability condition. The transformation of the nonlinear system into the specific form of the Lyapunov-Malkin theorem and the verification of the two conditions mentioned above requires a double perspective – analytical developments and numerical simulations – since the mathematical models are too complex to be approached only analytically. Accordingly, an important result is calculated, regarding an admissible delay threshold in preserving stability of the electrohydraulic servomechanism as vital system for the safety of the aircraft. Some considerations regarding the conservatism and the non-necessity of sufficient conditions conclude the work.
4. Lyapunov-Malkin type approach of equilibrium stability in a critical case applied to a switched model of a servomechanism with state delay – D. Enciu, A. Halanay, A. Toader, I. Ursu, accepted for publication in International Journal of Control
Abstract
A general theorem on equilibrium stability in a critical case is applied to switched strong nonlinear differential equations with time delay on state, characterizing electrohydraulic servomechanisms dynamics. Basically, its proof involves the use of the Lyapunov-Malkin approach to stability and multiple complete Lyapunov-Krasovskii functionals. The fulfilment of the equilibrium stability condition of the nonlinear system returns to the asymptotic stability condition of the linearized equations and to the so-called Lyapunov conditions for the latter. The transformation of the nonlinear system into the canonical form specific to the Lyapunov-Malkin theorem, and the verification of the two conditions mentioned above require analytical developments doubled by numerical simulations, since the mathematical models are too complex to be approached only analytically. As a consequence, an important result is obtained, for the first time, regarding the thresholds of admissible delay in preserving the stability of a real world object, vital for the safety of the aircraft.
Results – Phase II
Phase 2 „Development of mathematical models for systems of differential equations with delay and switching for the characterization of aeroelastic structures. Elaboration of necessary and sufficient stability conditions in the Lyapunov sense of equilibrium points for systems of differential equations with delay and switching – stability theorems” includes the following activities:
Act. 2.1 – Development of mathematical models for actuation of the primary control surfaces of the plane;
Act. 2.2 – The development of mathematical models for the active control of the wing in the wind tunnel;
Act. 2.3 – The method of polynomial Lyapunov functions for developing the necessary and sufficient stability condition;
Act. 2.4 – Horizon tour for other approaches to the necessary and sufficient conditions of stability.
The activities were carried out within Phase 2 with the achievement of the related Objective O2: obtaining necessary and sufficient conditions of stability in the Lyapunov sense for systems of linear and nonlinear differential equations with delay and switching. Thus, the framework is being prepared for the 3rd Phase of the project, that of the synthesis of active control laws and numerical simulations.
Stability is a sine qua non condition of every system. Therefore, the research effort is directed towards developing guaranteed stable systems. In the vast majority of cases, they are expressed through sufficient, conservative (restrictive) conditions, which sometimes impose drastic criteria, difficult to meet, and practically useless, because the system can be stable even if these criteria are not met. We are trying to find a unifying theory of both systems with delay and those with switching, so that the very important problem of reducing the conservatism of the sufficient conditions to ensure the stability of the equilibrium points.
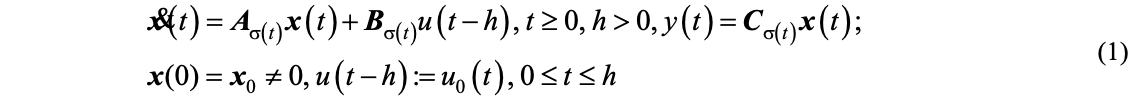
delayed system is reduced to a switching system without delay.
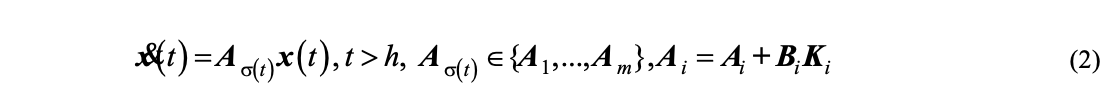
system for which we admit equilibrium point x(h) = 0
The contribution of this Phase is essentially summarized in:
1) demonstrating a proposition regarding the implementation of the delay avoidance condition through predictive state feedback;
2) a first theorem, giving a conservative stability condition, demonstrated in detail to understand the mechanisms of the theory;
3) a second theorem, quoted from the literature, giving a non-conservative but practically inoperative condition;
4) a third theorem, providing non-conservative stability conditions, but which requires the intervention of the computer in a process of mathematical convergence as in the famous problem of the four colours solved by Appel and Haken in 1976.
Results dissemination
1. WoS Article
A. Toader, I. Ursu, Daniela Enciu, G. Tecuceanu, Towards nonconservative conditions for equilibrium stability. Applications to switching systems with control delay, Communications in Nonlinear Science and Numerical Simulation, 121 (2023) 107188
2. BDI Proceedings
I. Ursu, A. Toader, G. Tecuceanu, Daniela Enciu, Input-to-state stability of a time-invariant system with control delay and additive disturbances, Proceedings in Applied Mathematics and Mechanics 2023;e202300152.
3. Control synthesis and stability analysis of equilibria in a mathematical model of a pneumatic servosystem – D. Enciu, A. Halanay, C.-A. Safta, A. Toader, I. Ursu, ICNPAA: Mathematical Problems in Engineering, Aerospace and Science (ICNPAA 2023), 27-30 June 2023, online
Abstract
A study on the stability of equilibrium points of a nonlinear system, representing the mathematical model of a pneumatic servomechanism, is developed. The characteristic equation of the linearized system appears to have a zero eigenvalue, therefore placing the problem in a critical case of stability. The solution requires the approach of Lyapunov-Malkin paradigm.
4. Input-to-state stability of a time-invariant system with control delay and additive disturbances – I. Ursu, A. Toader, G. Tecuceanu, D. Enciu, 93rd Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM 2023), 30 May – 2 June 2023, Dresden, Germany
Abstract
We consider a class of linear time invariant systems with control delay and additive disturbances. A state predictive feedback method is first applied to compensate the actuator delay. In this way, a closed loop system free of delay is achieved. It allows to ensure input-to-state-stability of the closed loop system. Applications are given for the lateral-directional stability of an airplane with two controls, on the aileron and on the rudder, in correlation with compliance with some regulatory flight conditions.
5. On a critical case for the stability of equilibria of a nonlinear switched system with state delay – D. Enciu, A. Halanay, I. Ursu, 5th International Applied Mathematics, Modelling and Simulation Conference (AMMS 2023), 14 -17 July 2023, Leipzig, Germany
Abstract
In this article, a stability problem in critical case is considered for a real world system, a hydraulic servomechanism, characterized by a nonlinear dynamic mathematical model, with state delay and structural switching. Solving the problem involves the use of the mathematical tool of Lyapunov Malkin critical stability, completed with the apparatus of multiple Lyapunov Krasovskii functionals. To apply this solution strategy, the mathematical model of the system is brought to the canonical form specific to the Lyapunov Malkin stability analysis. The stability condition of the nonlinear system returns to the fulfillment of the asymptotic stability condition of the linearized system, to which is added the fulfillment of a condition called the Lyapunov condition. The analysis of the fulfillment of these conditions is done analytically numeric. Finally, the conclusive result of the work consists in determining the critical delay of the system.
6. Further results on the input to state stability of a linear system with control delay – D. Enciu, I. Ursu, 12th International Conference on Pure and Applied Mathematics (ICPAM 2023), 17 – 21 July 2023, Porto, Portugal
Abstract
This paper presents a class of linear perturbed systems with control delay and for which stabilizing feedback is available. Through a Lyapunov-Krasovskii approach, by using the Jensen inequality, the Leibniz integral rule and a double Hadamard inequality, sufficient input-to-state stability conditions in terms of size of the delay is obtained.
7. On the stability of a time-invariant linear system with time-delay and disturbances with application to aerospace engineering – D. Enciu, I. Ursu, A. Toader, 30th Annual Conference on Applied and Industrial Mathematics (CAIM 2023), 14 – 18 September 2023, Iasi, Romania
Abstract
The beauty of the mathematical equations is highlighted by presenting a practical, real application in controlling the flight stability of an airplane in a turbulent atmospheric field. This paper presents a linear mathematical model with actuator delay in the control chain and external disturbances. The time-delay is compensated by applying a state predictive feedback method and the perturbation is treated according to the basic Kolmogorov concept.
8. The stability of a linear time-invariant system with control delay. Application to the stability of the aircraft control chain in conditions of atmospheric turbulence – A. Toader, D. Enciu, I. Ursu, 20th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2023), 12-16 November 2023, Rome, Italy
Abstract
A class of time-invariant linear systems with control delay and additive disturbances is considered. Through a predictive state feedback method, the control delay is compensated, reaching a closed-loop system without delay. Based on a theorem of F. Mazenc, S.-I. Niculescu, M. Krstic, stability is ensured in the presence of disturbances. The application is made on the control chain of an airplane, in the presence of Dryden-type atmospheric turbulence.
Rezultate – Etapa III
Phase 3 „Synthesis of active control laws. Numerical simulations” includes the following activities:
Act. 3.1 – Applications of active control on the mathematical model of an aircarft wing in the wind tunnel through numerical simulation
Act. 3.2 – Analysis of stability conditions.
The activities were carried out within Phase 3 with the achievement of the general Objective of developing a mathematical framework for obtaining necessary and sufficient conditions for the stability of the equilibrium points of differential equations with delay and switching with the reduction of the conservatism of the sufficient conditions given by the use of multiple Lyapunov-Krasovskii functionals and their application in the case of modeling some objects belonging to the real world – an airplane wing with aileron.
The main contributions are essentially summarized as:
- development of a unitary approach to the non-conservative stability of a linear switching system with control delay;
- using a state-predictive feedback control to convert the control-delayed switching system to a non-delayed switching system
- attesting the implementability of predictive state feedback control
- proving a theorem that provides a conservative condition of global uniform exponential stability as a starting point in the non-conservatism approach
- solution for the two equivalent variants obtained by discretization and the proof that the online operation and offline analysis versions give the same result, as expected
- solution for non-conservative LMI conditions by using SOS programming algorithms with the addition of a dwell time calculation algorithm given by a logic diagram
- applying, for the first time to our knowledge, nonconservatism theory based on SOS programming algorithms to a real-world object: a physical model of a smart airplane wing in a subsonic tunnel
- achieving a substantial result of the simulations: obtaining the guaranteed minimum dwell time that characterizes the equilibrium stability of the switching system with control delay
- the synthesis and application of a control law for the lateral-directional stability of an aircraft in the presence of a disturbance.
Results dissemination
WoS Article
Enciu, D.; Toader, A.; Ursu, I. Further Results on the Input-to-State Stability of a Linear Disturbed System with Control Delay. Mathematics, 2024, 12, 634. https://doi.org/10.3390/math12050634.

